
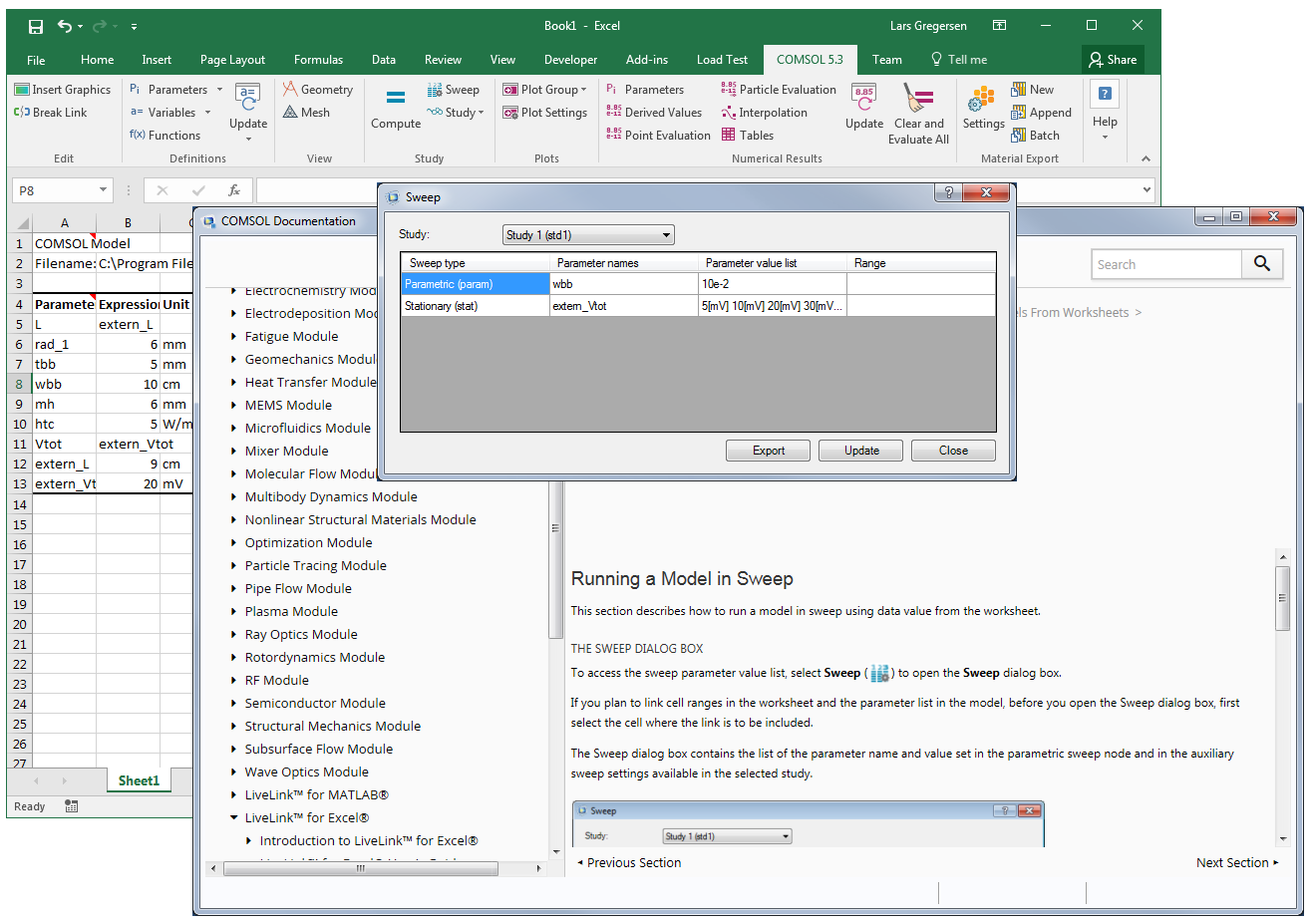
Since the coil wire does not extend to the boundary, there is no continuous path along which the current can flow.Īn invalid coil model. The image below illustrates one such invalid coil model. If you would try to impose a current flowing through an open circuit coil, that would be equivalent to implying that the current (electrons) instantaneously moves from one end of the open coil to the other, and this would violate Maxwell’s equations. Your models must satisfy this condition to be valid. Whenever you are modeling a coil, or any magnetic field excited by a current flow, you must have a closed path (loop) of current. An Important Modeling Condition: Closed Current Paths This brings us to one of the most basic points in coil modeling: the concept of a closed current path. The arrows show the current flowing through the wire and back along the surfaces truncating the modeling domain. As a consequence of the boundary condition, the current, which is flowing along the wire from one end to the other, will flow back along the surface of the modeling domain as shown in the image below. We will discuss the various possible boundary conditions, their physical interpretations, and why to use each one at length in a later blog post, but for this particular case, we will consider a boundary condition that represents a perfect electrical conductor.įor the physical interpretation of this, we assume that our coil sits inside of a cylindrical metal container. We need to consider some boundary conditions along the boundaries of the cylinder or whatever surrounding domain shape we choose. This choice of finite-sized region introduces another assumption at the boundaries. Although it will never be precisely zero, we can reasonably truncate our modeling domain to a finite-sized space.īy choosing a finite modeling region around the coil, we are assuming that we are only interested in the fields in this region. The field intensity will drop off with the inverse of distance to a straight wire, so the field magnitude will be quite small far away from the coil. This is a finite-sized domain, yet the magnetic field will actually extend infinitely far away from the coil. This is the computational domain within which we are solving for the magnetic field. First, we can see that there is a cylinder around the coil representing the air domain. There are actually a couple of other assumptions that have gone into solving the above model. The current flow (black arrows) in the wire results in a magnetic field (colored arrows) in the surrounding air region. Based upon these two assumptions, we will say that a reasonable computational model of a coil might look like the image below, which shows a single wire with a single turn as well as the surrounding magnetic field due to the current flow.Ī computational model of a coil with one turn.
We also won’t concern ourselves with the wires between the coil and the source, but assume that they are electrically insignificant. Instead, we will just assume that a device exists that provides a constant voltage, or a constant current.
#COMSOL 5.3 DOCUMENTATION VIEW HOW TO#
We are interested in learning how to model this magnetic field and how it interacts with other objects.įor the purpose of learning coil modeling, we won’t concern ourselves with exactly what is happening within the source itself. This is a vector field, having both a magnitude and direction, and can be computed from Ampère’s law. This problem can be solved using the finite element method as implemented in the AC/DC Module in COMSOL Multiphysics.Īs a consequence of the computed current flow, a magnetic field arises and surrounds the wire. Current cannot flow in or out of the wire anywhere else, so the electric insulation condition is applicable on the remaining boundaries. The magnitude and direction of this current throughout the conductor can be computed from Ohm’s law and the Charge conservation equation, along with a set of boundary conditions.Ī very simple electromagnetic coil connected to a DC voltage source.įor this single wire, we can consider a grounded boundary condition at one end, meaning an electric potential of zero, and a higher electric potential on the other end. Due to the voltage difference, a current will flow through the wire. Let’s start with a simple example of a conductive wire that is bent into a loop and connected to a constant voltage source, a battery (shown below). How to Model a Basic Coil in COMSOL Multiphysics

If your work involves modeling coils, you will need a complete understanding of this topic. Today, we will look into one of the key concepts to keep in mind when modeling coils: closing the current loop. One of the most common uses of the AC/DC Module is for modeling electromagnetic coils and the interactions with their surroundings.


 0 kommentar(er)
0 kommentar(er)
